A.    SEGIEMPAT

       Segi empat adalah suatu bidang datar yang dibentuk/dibatasi oleh empat garis lurus sebagai sisinya. Bangun datar segi empat yang akan dibahas meliputi persegi panjang, persegi, jajargenjang, belah ketupat, layang-layang dan trapesium. Sedangkan persegi panjang adalah segi empat dengan sisi-sisi yang berhadapan sejajar dan sama panjang, serta keempat sudutnya siku-siku.

1.    Jenis - Jenis Dan Sifat Segiempat

1.1    Jenis - Jenis Segiempat

  • Segiempat beraturan atau persegi

  • Persegi panjang

  • Jajargenjang

  • Trapesium

  • Belah ketupat

  • Layang - layang

     

1.2    Sifat - Sifat Segiempat

1.      Persegi

  

Persegi adalah persegi panjang yang keempat sisinya sama panjang.

Sifat-sifat persegi, antara lain:

1) Persegi adalah persegi panjang

2) Sisi-sisi yang berhadapan sama panjang dan sejajar

3) Keempat sudutnya siku-siku

4) Panjang diagonal-diagonalnya  sama dan saling membagi dua sama panjang

5) Panjang keempat sisinya sama

6) Setiap sudutnya dibagi dua sama besar oleh diagonal-diagonalnya

7) Diagonal-diagonalnya berpotongan saling tegak lurus 

8) Memiliki empat buah sumbu simetri

9) Memiliki empat buah sumbu putar


Rumus :
Luas = s x s
Keliling = s + s + s + s
              = 4s

Jumlah simetri lipat = 4  

Jumlah simetri putar = 4

 

2. Persegi Panjang 

 

Persegi Panjang adalah suatu segi empat yang kempat sudutnya berbentuk siku-siku dan sisi-sisi yang saling berhadapan sama panjang.

Sifat-sifat persegi panjang, antara lain:

1) Panjang sisi-sisi yang berhadapan sama

2) Keempat sudutnya siku-siku

3) Panjang diagonal-diagonalnya sama dan saling membagi dua sama panjang 

4) Memiliki dua pasang sisi yang saling sejajar (AB sejajar CD dan AD sejajar BC)

5) Memiliki empat buah sudut siku-siku ( besar 90⁰ )

6) Memiliki dua buah sumbu simetri

7) Memiliki dua buah simetri putar


Rumus :
Luas = p x l
Keliling = p + p + l + l
               = 2p + 2l
               = 2 (p+l)

Jumlah Simetri Lipat = 2 

Jumlah Simetri Putar = 2

 

3.    Jajar genjang 

 

 

Jajar genjang adalah segi empat yang setiap panjang sisi yang berhadapan sama panjang dan sejajar.

Sifat-sifat jajar genjang, antara lain:

1)    Sisi-sisi yang berhadapan pada suatu jajargenjang sama panjang dan sejajar

2)     Sudut-sudut berhadapan pada suatu jajargenjang sama besar ( ∠A = ∠C dan ∠B = ∠D )

3)    Sudut-sudut yang berdekatan pada suatu jajargenjang jumlahnya 180o

4)    Diagonal-diagonal suatu jajar genjang saling membagi dua sama panjang

5)    Tidak memiliki sumbu simetri

6)    Memiliki dua buah simetri putar 

Rumus :
Luas = a x t
Keliling = a+a+b+b
              = 2a + 2b
              =2 (a + b)

 Jumlah simetri lipat = 0 

 Jumlah simetri putar = 2

 

4.    Trapesium

 

Trapesium adalah segi empat yang memiliki paling sedikit satu pasang ruas garis yang sejajar.  

Sifat-sifat trapesium meliputi:

1)    Memiliki sepasang sisi sejajar

2)   Memiliki dua diagonal yang berpotongan 

3)   Memiliki empat sudut yang jumlahnya 360⁰

4)   Jumlah dua sudut diantara dua sisi sejajar adalah 180⁰

Jenis-jenis trapesium ada tiga macam sebagai berikut.

a.    Trapesium Siku - Siku

  Sifat trapesium siku-siku :

1)    Memiliki sepasang sisi sejajar, yaitu sisi AB dan sisi DC

2)    Memiliki dua buah diagonal, AC dan BD

3)    Kedua diagonalnya tidak sama panjang

4)    Memiliki dua sudut siku-siku (∠90°) yang berdekatan, yaitu sudut ∠A
(∠BAD) dan ∠D (∠CDA)

5)    Memiliki sebuah sudut tumpul, yaitu ∠C (∠BCD)

6)    Memiliki sebuah sudut lancip, yaitu ∠B (∠ABC)

7)    Jumlah keempat sudutnya 360° (∠A + ∠B + ∠C + ∠D = 360°)

8)    Tidak memiliki sumbu simetri

9)    Tidak memiliki simetri putar

 

b.    Trapesium Sama Kaki

 

Sifat trapesium sama kaki : 

a. Memiliki sepasang sisi sejajar, yaitu sisi AB dan sisi CD 

b. Memiliki sepasang sisi sama panjang, yaitu sisi AD dan BC 

c. Memiliki dua buah diagonal yang sama panjang, AC = BD 

d. Sudut yang berdekatan sama besar, ∠A = ∠B dan ∠C = ∠D 

e. Memiliki dua sudut tumpul, yaitu ∠A (∠DAB) dan ∠B (ABC)f. Memiliki dua buah sudut lancip, yaitu ∠C (∠BCD) dan ∠D (∠CDA) 

g. Jumlah keempat sudutnya 360° (∠A + ∠B + ∠C + ∠D = 360°) 

h. Memiliki satu buah sumbu simetri 

i. Tidak memiliki simetri putar       

 

Sumbu Simetri Trapesium Sama Kaki ABCD

 

c.    Trapesium Sembarang

 

Sifat trapesium sembarang :

a. Memiliki sepasang sisi sejajar, yaitu sisi AB dan sisi CD 

b. Memiliki dua buah diagonal, AC dan BD 

c. Kedua diagonalnya tidak sama panjang 

d. Keempat sudutnya tidak sama besar 

e. Jumlah keempat sudutnya 360° (∠A + ∠B + ∠C + ∠D = 360°) 

f. Tidak memiliki sumbu simetri 

g. Tidak memiliki simetri putar    

Rumus:
Luas = ½ x (a+b) x t
 Keliling = AB + BC + CD + AD

Jumlah simetri lipat 

Pada trapesium sama kaki = 1 

Pada trapesium siku-siku = 0 

Jumlah simetri putar = 1

 

5.    Belah Ketupat

Belah ketupat adalah segi empat yang memiliki dua pasang ruas garis yang sejajar dan keempat ruas garisnya sama panjang. 

 

Sifat-sifat belah ketupat, antara lain:

a. Memiliki empat buah sisi yang sama panjang (AB = BC = CD = DA) 

b. Memiliki dua pasang sisi yang saling sejajar (AB sejajar CD dan AD sejajar BC) 

c. Memiliki dua garis diagonal yang saling berpotongan tegak lurus AC ⊥ BD , tetapi panjangnya berbeda. Diagonal-diagonal tersebut saling membagi sama panjang AO = OC dan OB = OD
Mempunyai empat buah sudut dengan sudut-sudut yang berhadapan sama besar ( ∠A = ∠C dan ∠B = ∠D ) 

d. Jumlah dua sudut yang berdekatan adalah 180⁰
∠A + ∠B = ∠B +∠C = ∠C + ∠D = ∠A +∠D = 180⁰

e. Memiliki dua buah sumbu simetri
• Simetri lipat pertama: B-D. B bertemu dengan D dengan AC sebagai sumbu
simetri.
• Simetri lipat kedua: A-C. A bertemu dengan C dengan BD sebagai sumbu
simetri. 

f. Memiliki dua buah simetri putar

Rumus:

Luas = ½ x d1 x d2
Keliling = AB + BC + CD + AD

 Jumlah simetri lipat = 2 

Jumlah simetri putar = 2

 

6.    layang - Layang

 

Layang-layang adalah segi empat yang memiliki dua pasang sisi yang sama panjang. 

Sifat layang-layang, antara lain:

a. Memiliki dua pasang sisi yang sama panjang (AB = AD dan CB = CD) 

b. Dibentuk oleh dua buah segitiga sama kaki, yaitu segitiga ABD dan segitiga CDB

 c. Memiliki dua garis diagonal yang saling berpotongan tegak lurus AC ⊥ BD, tetapi panjangnya berbeda. Diagonal AC membagi BD sama panjang (OB = OD)

d. Memiliki empat buah sudut yang sepasang sudutnya sama besar (∠B = ∠D) dan sepasang lainnya tidak 

e. Memiliki satu buah sumbu simetri

f. Memiliki satu buah simetri putar

Rumus:

Luas = ½ x d1 x d2
 Keliling = AB + BC + CD + AD

 Jumlah simetri lipat = 1 

Jumlah simetri putar = 1


B.    SEGITIGA

Jenis-jenis segitiga berdasarkan panjang sisinya:

1. Segi tiga sama sisi

 

Suatu segitiga dikatakan segitiga sama sisi jika dan hanya jika memiliki tiga ukuran sisi yang sama panjang.

Sifat-sifat segitiga sama sisi, yaitu: 

a. Ketiga sisinya sama panjang 

b. Sudut-sudutnya sama besar, masing masingg memiliki besar sudut 60⁰

c. Memiliki tiga garis diagonal sisi yang berpotongan tepat di satu titik 

d. Memiliki tiga sumbu simetri 

e. Memiliki tiga sumbu putar 

2. Segi tiga sama kaki 

 

Suatu segitiga dikatakan segitiga sama kaki jika dan hanya jika memiliki paling sedikit dua ukuran sisi yang sama panjang.

Sifat-sifat segitiga sama kaki, yaitu: 

a. Dua buah sisinya sama panjang 

b. Memiliki dua buah sudut sama besar 

c. Memiliki sebuah sumbu simetri 

d. Memiliki sebuah sumbu putar

3. Segi tiga sembarang

 

Segitiga yang panjang sisi-sisinya tidak mencirikan segitiga sama kaki maupun samasisi disebut segitiga sembarang. Segitiga sembarang adalah segitiga yang ketigasisinya tidak sama panjang dan besar ketiga sudutnya juga tidak sama.

Sifat-sifat segitiga sembarang, yaitu: 

a. Memiliki panjang ketiga sisinya berlainan 

b. Memiliki besar ketiga sudutnya tidak sama

Disebut segitiga sembarang yaitu jika tidak ada sisi yang sama panjang.

Jumlah simetri lipat = 0 

Jumlah simetri putar = 1  

 

Jenis-jenis segitiga berdasarkan besar sudut-sudutnya: 

1. Segitiga Siku-siku

 

Segitiga siku-siku adalah segitiga yang salah satu sudutnya memiliki ukuran sudut sama dengan 90⁰.

 2. Segitiga Tumpul   

 

Segitiga tumpul adalah segitiga yang salah satu sudutnya memiliki ukuran sudut sama dengan lebih dari 90⁰ tapi kurang dari 180⁰. 

3. Segitiga Lancip

 

Segitiga lancip adalah segitiga yang ketiga ukuran sudutnya < 90⁰.

Rumus:
Luas = ½ x a x t
Keliling = a + b + c 

 Jumlah simetri lipat 

Segitigi sama sisi = 3

Segitiga sama kaki = 1

Segitiga sembarang = 0 

Jumlah simetri putar 

Segitiga sama sisi = 3

Segitiga sama kaki = 1

Segitiga sembarang = 0

Teorema Pythagoras

Pythagoras menyatakan bahwa “ untuk setiap segitiga siku-siku berlaku kuadrat panjang sisi miring (Hipotenusa) sama dengan jumlah kuadrat panjang sisi siku-sikunya”.

Berdasarkan teorema Pythagoras berlaku:

c2 = a2 + b2

atau

keterangan:

c = panjang sisi miring (Hipotenusa)

a = tinggi

b = alas

sisi AC dan AB membentuk siku-siku

Kegunaan Teorema Pythagoras

Teorema Pythagoras selain untuk menghitung panjang salah satu sisi segitiga yang tidak diketahui, juga digunakan untuk menghitung sebagai berikut:

  1. Panjang diagonal persegi dan persegi panjang
    Perhatikan gambar berikut ini!

    Untuk bangun di atas berlaku teorema Pythagoras:
    AC2 = AB2 + BC2
    AC2 = AD2 + CD2
  2. Panjang diagonal ruang pada kubus dan balok
    Perhatikan gambar di bawah ini!

    Untuk bangun ruang di atas berlaku teorema Pythagoras sebagai berikut:
    AG2 = AC2 + CG2 Keterangan:
    AG = diagonal ruang
    CG = tinggi balok
    AC = diagonal bidang alasUntuk mencari panjang AC, berlaku sebagai berikut:
    AC2 = AB2 + BC2Keterangan:
    AC =diagonal persegi panjang ABCD
    AB = panjang balok
    BC = lebar balokMaka dapat dirumuskan kembali sebagai berikut:
    AG2 = AC2 + CG2
    AG2 =  AB2 + BC2 + CG2
    dr2 = p2 + l2 + t2Keterangan:
    dr = diagonal ruang
    p = panjang
    l = lebar
    t = tinggi
  3. Mencari jarak dua titik pada bidang koordinat
    Perhatikan gambar berikut!

C.    LINGKARAN

Lingkaran adalah tempat kedudukan titik-titik yang berjarak sama dengan satu titik tertentu.  Yang dimaksud titik tertentu adalah titik pusat lingkaran, sedangkan jarak yang sama adalah jari-jari lingkaran.

Ciri-ciri lingkaran ialah memiliki diameter yang membaginya menjadi dua sisi seimbang dan memiliki jumlah sudut sebesar 180 derajat. Selain itu, diameter konstan dan jari-jari yang menghubungkan titik pusat dengan titik busur lingkaran juga menjadi ciri-ciri dari sebuah lingkaran.

Lingkaran memiliki satu sisi dengan simetri lipat lingkaran yang tak terhingga sebagai salah satu sifatnya. Kemudian sifat lingkaran juga memiliki simetri putar lingkaran yang tak terhingga.

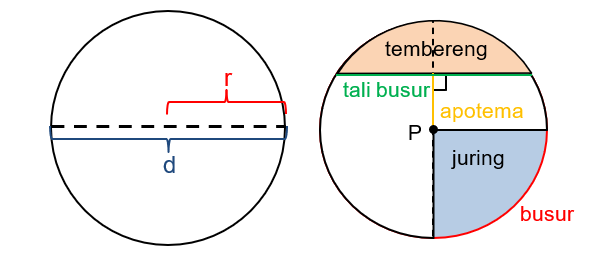
Unsur-unsur Lingkaran


 

Titik Pusat (P)

Titik pusat merupakan unsur lingkaran pertama yang perlu kamu ketahui. Titik yang berada tepat di bagian tengah lingkaran disebut titik pusat.

Jarak titik pusat dengan semua titik pada bangun datar yang satu ini selalu sama. Titik pusat kerap disimbolkan dengan penggunaan huruf kapital, seperti A, O, P, Q, dan lain sebagainya.

Jari-jari Lingkaran (r)

Unsur selanjutnya ialah jari-jari lingkaran. Jari-jari dapat diartikan sebagai jarak antara titik pusat lingkaran dengan titik pada lingkaran.

Panjang jari-jari pada sebuah lingkaran selalu sama karena jarak antara titik pusat dengan semua titik pada lingkaran sama. Dalam rumus matematika, jari-jari kerap disimbolkan dengan huruf r atau yang disebut radius. Karena panjangnya sama saja, jarak ini bisa terbentang ke bawah, ke atas, ke kanan, maupun ke kiri.

Diameter (d)

Diameter adalah unsur lingkaran berikutnya yang akan dibahas. Panjang garis lurus yang menghubungkan dua titik pada keliling lingkaran dan melalui titik pusat lingkaran dapat diartikan sebagai diameter.

Dapat dikatakan bahwa nilai diameter lingkaran merupakan dua kali nilai jari-jari lingkaran. Begitu pun sebaliknya, jari-jari lingkaran memiliki nilai setengah dari diameter. Dalam rumus matematika, diameter kerap disimbolkan dengan huruf d. 

Busur

Unsur lingkaran berikutnya ialah busur. Apa yang dimaksud dengan busur sebagai unsur lingkaran? Bagian lingkaran yang berbentuk garis lengkung merupakan pengertian dari busur.

Jenis busur dalam lingkaran terbagi menjadi dua, yakni busur besar dan busur kecil. Busur yang panjangnya lebih dari setengah keliling lingkaran disebut sebagai busur besar.

Sementara busur yang panjangnya kurang dari setengah keliling lingkaran disebut busur kecil. Garis lengkung, baik terbuka maupun tertutup dan saling berhimpit dengan lingkaran disebut busur lingkaran.

Tali Busur

Unsur-unsur lingkaran yang selanjutnya ialah tali busur. Garis lurus yang menghubungkan dua titik pada lingkaran disebut sebagai tali busur.

Garis lurus tersebut mengaitkan dua titik pada keliling lingkaran, tetapi tidak melewati titik pusat lingkaran. Jika Grameds kesulitan membayangkannya, bayangkan saja sebuah tali busur lingkaran sama seperti tali pada busur panah.

Juring

Daerah yang diapit oleh dua jari-jari dan busur lingkaran merupakan pengertian dari juring sebagai unsur lingkaran. Juring pada lingkaran terdiri atas dua bagian, yakni juring besar dan juring kecil.

Dimana daerah dalam lingkaran yang dibatasi jari-jari dan busur besar lingkaran disebut juring besar. sementara daerah dalam lingkaran yang dibatasi jari-jari dan busur kecil disebut sebagai juring kecil.

Tembereng

Daerah yang diapit oleh tali busur dan busur lingkaran dapat diartikan sebagai tembereng. Kemudian tembereng terbagi menjadi dua, yakni tembereng besar dan tembereng kecil.

Daerah yang dibatasi oleh tali busur dan busur besar lingkaran disebut sebagai tembereng besar. Sedangkan daerah yang dibatasi oleh tali busur dan busur kecil lingkaran disebut tembereng kecil.

Apotema

Apotema menjadi unsur lingkaran yang akan dibahas. Ruas garis tegak lurus yang menghubungkan titik pusat lingkaran dengan tali busur lingkaran diartikan sebagai apotema. Kemudian apotema juga dapat diartikan sebagai jarak terpendek tali busur dengan titik pusat lingkaran.

Sudut Pusat

Sudut pusat adalah unsur lingkaran selanjutnya yang akan dibahas. Sebuah sudut yang terbentuk karena pertemuan antara dua tali busur dengan satu titik pada keliling lingkaran disebut sebagai sudut pusat.

Sudut Keliling

Sudut keliling adalah unsur lingkaran selanjutnya yang akan dibahas. Sudut yang dibentuk oleh perpotongan antara dua buah tali busur di suatu titik pada keliling lingkaran dapat dikatakan sebagai sudut keliling.

Rumus Lingkaran

1. Rumus Keliling Lingkaran

jika yang dicari adalah jari-jari lingkaran dengan keliling lingkaran.

 

2. Rumus Luas Lingkaran

 

jika yang dicari adalah jari-jari lingkaran dengan luas lingkarannya.

 

Rumus Luas Juring Lingkaran

Untuk mencari luas juring lingkaran, elo bisa kalikan luas lingkaran dengan hasil bagi sudut pusat dibagi 360°.

LJ = (Menghitung Luas Juring dan Tembereng Pada Lingkaran 129) x π x r2

Dengan keterangan:

LJ = Luas Juring

a = sudut pusat

π = 3,14 atau Menghitung Luas Juring dan Tembereng Pada Lingkaran 130

r = jari-jari lingkaran

Rumus Luas Tembereng Lingkaran

Untuk mencari luas tembereng pada lingkaran cukup mudah, kita tinggal selisihkan luas juring dan luas segitiga. 

 

Jadi, rumus mencari tembereng yaitu:

LT = LJ – LΔ

Dengan keterangan:

LT = Luas Tembereng

Rumus Apotema Lingkaran

Apa itu apotema lingkaran sudah dijelaskan dengan lengkap diatas. Pada sebuah lingkaran, untuk mencari panjang dari garis tegak lurus ini memiliki rumus.

Rumus apotema lingkaran yaitu sebagai berikut :

rumus apotema lingkaran

Keterangan :
r = jari jari lingkaran
a = tali busur lingkaran

Rumus Sudut Pusat

Rumus sudut pusat lingkaran yaitu sebagai berikut :

Sudut Pusat Lingkaran = 2 × Sudut Keliling Lingkaran

Rumus Sudut Keliling

Rumus sudut keliling lingkaran yaitu sebagai berikut :

Sudut Keliling Lingkaran = 1/2 × Sudut Pusat Lingkaran

 

 

LJ = Luas Juring

LΔ = Luas segitiga