Pengertian Pola Bilangan

 

Pola Bilangan

---

Bukalah mata dengan serius sejenak, lihat susunan bilangan-bilangan di bawah ini:
$1,3,5,7,9,11,13,15,17,19,21,\cdots$

$2,4,6,8,10,12,14,16,18,20,22,\cdots$

Coba kita amati dan pikirkan. Ada sesuatu yang konsisten, ada sebuah bentuk, ada sebuah pola yang terus-menerus, sehingga kita bisa menebak angka-angka selanjutnya, bukan?

Jadi, kita definisikan pengertian pola bilangan ini sebagai:

Pola bilangan adalah susunan angka yang membentuk pola tertentu (secara konsisten dan terus-menerus).

Jenis Pola Bilangan

Secara umum, kita akan mempelajari setidaknya 9 bentuk pola bilangan:

1. Ganjil
2. Genap
3. Aritmetika
4. Geometri
5. Persegi
6. Persegi Panjang
7. Segitiga
8. Fibonacci
9. Pascal

2.1 Ganjil

$U_n=2n-1$

Salah satu yang kita lihat di atas, dengan pola:
$1,3,5,7,\cdots$

2.2 Genap

$U_n=2n$

Pola bilangan genap merupakan pola kelipatan dua.
$2,4,6,8,\cdots$

2.3 Aritmetika

$U_n=a+(n-1)b$

Pola bilangan aritmetika merupakan pola susunan di mana bilangan awal berubah teratur secara aritmetik (dengan beda; perhitungan satu dimensi; operasi tambah atau kurang).
$7,12,17,22,27,\cdots$

2.4 Geometri

$U_n=a\cdot r^{n-1}$

Pola bilangan geometri merupakan pola susunan di mana bilangan awal berubah teratur secara geometri (dengan rasio; perhitungan lebih dari satu dimensi; operasi kali atau bagi).
$6,12,24,48,\cdots$

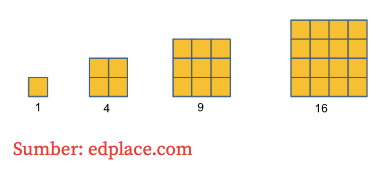
2.5 Persegi

Pola bilangan yang ditata dengan aturan pembentuk persegi, dan dirumuskan:

$U_n=n^2$

2.6 Persegi Panjang

Dirumuskan:

$U_n=n(n+1)$

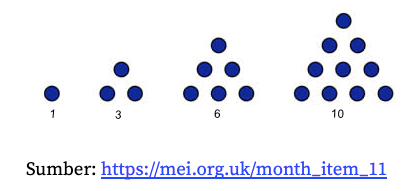
2.7 Segitiga

Dirumuskan:

$U_n=\frac{1}{2}n(n+1)$

2.8 Fibonacci

Fibonacci adalah barisan bilangan yang berawal 0 dan 1, kemudian angka berikutnya didapat dengan cara menambahkan kedua bilangan yang berurutan sebelumnya. Apabila dirumuskan:

$\begin{array}{c}{U}_n=\{\begin{array}{ccc}0,& & \text{jika}n=1\\ 1,& & \text{jika}n=2\\ U(n-1)+U(n-2),& & \text{jika}n\ne \{1,2\}\end{array}\end{array}$

Maka, barisan bilangan Fibonacci sebagai berikut.
$0,1,1,2,3,5,8,13,21,34,55,\cdots$

2.9 Segitiga Pascal

$U_n=2^{n-1}$

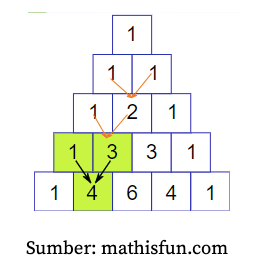
Terakhir, ada yang namanya pola bilangan Pascal. Mungkin banyak di antara kamu gak asing dengan nama Pascal. Yap, ditemukan oleh Blaise Pascal, seorang ilmuwan asal Prancis. Kita mengenalnya sebagai Segitiga Pascal. Lalu, apa hubungannya dengan pola bilangan? Segitiga Pascal merupakan suatu pola bilangan. Kamu bisa melihatnya dari berbagai peraturan atau ketentuannya di sini:

• Baris paling atas ditulis satu kotak saja, yaitu 1.
• Setiap baris dalam segitiga pascal selalu diawali dan akan diakhiri oleh angka 1.
• Jumlah kotak selanjutnya dalam segitiga pascal ini ditulis di baris ke-2 sampai ke-n adalah hasil penjumlahan dua bilangan diagonal di atasnya.
• Setiap baris akan membentuk simetris.
• Banyak bilangan di setiap barisnya memiliki kelipatan dua dari jumlah angka baris sebelumnya.

Sangat unik, bukan? Supaya lebih terbayang, kam

u bisa lihat gambar berikut.

---

---