Pengertian Deret Bilangan

Deret Bilangan

Salah satu hal mendasar tentang deret adalah kita bisa menemukan jumlah suku-suku yang terdapat dalam suatu barisan. Oleh karena itu, bukankah kita punya definisi jelas tentang deret?

Deret adalah penjumlah suku dalam suatu barisan, yang disimbolkan dengan: $S_{n}$

. Kita bisa melihat bentuk umumnya di bawah ini:

U_{1} + U_{2} + U_{3} + \dots + U_{n} = S_{n}

4.1 Deret Aritmetika

Deret aritmetika merupakan penjumlahan suku-suku dalam suatu barisan aritmetika. Masih ingat ciri barisan aritmetika, 'kan?

$\begin{aligned} (1)... & S_{n} = \frac{n}{2} (a + U_{n}) \\ (2)... & S_{n} = \frac{n}{2} (2 a + (n - 1) b) \\ (3)... & b = U_{n} - U_{n - 1} \\ (4)... & b = \frac{U_{p} - U_{q}}{p - q} \end{aligned}$

Keterangan:

$S_{n}$

= jumlah suku ke-

n

= suku awal atau

U_{1}

= sembarang suku dalam barisan

Perhatikan bilangan di bawah ini:

$3, 7, 11, 15, 19, \dots$

Tentukanlah jumlah suku ke-11 dari barisan bilangan di atas!

PENYELESAIAN.

Diketahui: $a = U_{1} = 3$

Ditanya: $S_{11} = \dots ?$

Dijawab:
$\begin{aligned} i)... b & = U_{n} - U_{n - 1} \\ = U_{2} - U_{1} \\ = 7 - 3 \\ b & = 4 \end{aligned}$

$\begin{aligned} ii)... S_{n} & = \frac{n}{2} (2 a + (n - 1) b) \\ S_{11} & = \frac{11}{2} (2 (3) + (11 - 1) 4) \\ = \frac{11}{2} {(46)}^{23} \\ S_{11} & = 253 \end{aligned}$

\begin{aligned} ii)... S_{n} & = \frac{n}{2} (2 a + (n - 1) b) \\ S_{11} & = \frac{11}{2} (2 (3) + (11 - 1) 4) \\ = \frac{11}{2} {(46)}^{23} \\ S_{11} & = 253 \end{aligned}

\begin{aligned} ii)... S_{n} & = \frac{n}{2} (2 a + (n - 1) b) \\ S_{11} & = \frac{11}{2} (2 (3) + (11 - 1) 4) \\ = \frac{11}{2} {(46)}^{23} \\ S_{11} & = 253 \end{aligned}

4.2 Deret Geometri

Deret geometri merupakan penjumlahan suku-suku dalam suatu barisan geometri, yang berciri terdapat rasio antarsuku. Berikut rumus yang berlaku:

$\begin{aligned} (1)... & S_{n} = \frac{a (r^{n} - 1)}{r - 1}, untuk r > 1 \\ (2)... & S_{n} = \frac{a (1 - r^{n})}{1 - r}, untuk r < 1 \\ (3)... & r = \frac{U_{n}}{U_{n - 1}} \end{aligned}$

Keterangan:

$S_{n}$

= jumlah suku ke-

n

= suku awal atau

U_{1}

= suku ke-

n

Perhatikan bilangan di bawah ini:

$243, 81, 27, 9, \dots$

Tentukanlah jumlah suku ke-4 dari barisan bilangan di atas!

PENYELESAIAN.

Diketahui: $a = U_{1} = 243$

Ditanya: $S_{4} = \dots ?$

Dijawab:
$\begin{aligned} i)... r & = \frac{U_{n}}{U_{n - 1}} \\ = \frac{U_{2}}{U_{1}} \\ = \frac{81}{243} \\ r & = \frac{1}{3} kita ketahui r < 1 \end{aligned}$

$\begin{aligned} ii)... S_{n} & = \frac{a (1 - r^{n})}{1 - r} \\ S_{4} & = \frac{243 (1 - {(\frac{1}{3})}^{4})}{1 - \frac{1}{3}} \\ = \frac{243 - 243^{3} \cdot (\frac{1}{81})}{\frac{2}{3}} \\ = \frac{240}{\frac{2}{3}} \\ = 240^{120} \cdot \frac{3}{2} \\ S_{4} & = 360 \end{aligned}$

\begin{aligned} ii)... S_{n} & = \frac{a (1 - r^{n})}{1 - r} \\ S_{4} & = \frac{243 (1 - {(\frac{1}{3})}^{4})}{1 - \frac{1}{3}} \\ = \frac{243 - 243^{3} \cdot (\frac{1}{81})}{\frac{2}{3}} \\ = \frac{240}{\frac{2}{3}} \\ = 240^{120} \cdot \frac{3}{2} \\ S_{4} & = 360 \end{aligned}

\begin{aligned} ii)... S_{n} & = \frac{a (1 - r^{n})}{1 - r} \\ S_{4} & = \frac{243 (1 - {(\frac{1}{3})}^{4})}{1 - \frac{1}{3}} \\ = \frac{243 - 243^{3} \cdot (\frac{1}{81})}{\frac{2}{3}} \\ = \frac{240}{\frac{2}{3}} \\ = 240^{120} \cdot \frac{3}{2} \\ S_{4} & = 360 \end{aligned}

\begin{aligned} ii)... S_{n} & = \frac{a (1 - r^{n})}{1 - r} \\ S_{4} & = \frac{243 (1 - {(\frac{1}{3})}^{4})}{1 - \frac{1}{3}} \\ = \frac{243 - 243^{3} \cdot (\frac{1}{81})}{\frac{2}{3}} \\ = \frac{240}{\frac{2}{3}} \\ = 240^{120} \cdot \frac{3}{2} \\ S_{4} & = 360 \end{aligned}

\begin{aligned} ii)... S_{n} & = \frac{a (1 - r^{n})}{1 - r} \\ S_{4} & = \frac{243 (1 - {(\frac{1}{3})}^{4})}{1 - \frac{1}{3}} \\ = \frac{243 - 243^{3} \cdot (\frac{1}{81})}{\frac{2}{3}} \\ = \frac{240}{\frac{2}{3}} \\ = 240^{120} \cdot \frac{3}{2} \\ S_{4} & = 360 \end{aligned}

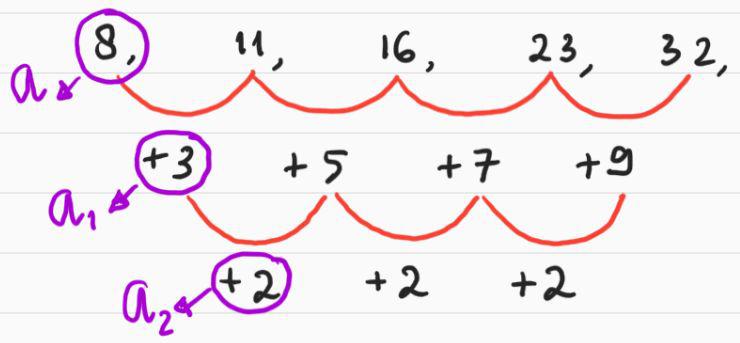
4.3 Deret Aritmetika Bertingkat

Deret aritmetika bertingkat merupakan penjumlahan suku-suku dalam barisan aritmetika bertingkat. Berikut rumus-rumus yang bisa digunakan:

$\begin{aligned} (1)... & S_{n} = n \cdot a + \frac{n (n - 1)}{1 \cdot 2} \cdot a_{1} + \frac{n (n - 1) (n - 2)}{1 \cdot 2 \cdot 3} \cdot a_{2} \\ (2)... & S_{n} = n \cdot a + \frac{n (n - 1)}{1 \cdot 2} \cdot a_{1} + \frac{n (n - 1) (n - 2)}{1 \cdot 2 \cdot 3} \cdot a_{2} + \frac{n (n - 1) (n - 2) (n - 3)}{1 \cdot 2 \cdot 3 \cdot 4} \cdot a_{3} \\ (3)... & S_{n} = n \cdot a + \frac{n (n - 1)}{1 \cdot 2} \cdot a_{1} + \frac{n (n - 1) (n - 2)}{1 \cdot 2 \cdot 3} \cdot a_{2} + \dots + \frac{n (n - 1) (n - 2) \dots}{1 \cdot 2 \cdot 3 \cdot \dots} \cdot a_{r} \end{aligned}$

Keterangan:

(1) = rumus deret tingkat 2
(2) = rumus deret tingkat 3
(3) = rumus deret tingkat $r$

(

1, 2, \dots, r

= jumlah suku ke-

n

= selisih awal di tingkat

r

(

1, 2, \dots, r

)

Perhatikan bilangan di bawah ini:

$8, 11, 16, 23, 32, \dots$

Tentukanlah jumlah suku ke-20 dari barisan bilangan di atas!

PENYELESAIAN.

Diketahui: barisan aritmetika tingkat 2 ; $a = 8$

;

a_{1} = 3

;

a_{2} = 2

Persamaan dan Pertidaksamaan Linear Satu Variabel | Materi, Soal dan Pembahasan | Matematika SMP VII

Ditanya: $S_{20} = \dots ?$

Dijawab:
$\begin{aligned} i)... S_{n} & = n \cdot a + \frac{n (n - 1)}{1 \cdot 2} \cdot a_{1} + \frac{n (n - 1) (n - 2)}{1 \cdot 2 \cdot 3} \cdot a_{2} \\ S_{20} & = 20 \cdot 8 + \frac{20^{10} (19)}{2} \cdot 3 + \frac{20 \cdot (19) \cdot {(18)}^{3}}{6} \cdot 2 \\ = 160 + 570 + 2280 \\ S_{20} & = 3010 \end{aligned}$

\begin{aligned} i)... S_{n} & = n \cdot a + \frac{n (n - 1)}{1 \cdot 2} \cdot a_{1} + \frac{n (n - 1) (n - 2)}{1 \cdot 2 \cdot 3} \cdot a_{2} \\ S_{20} & = 20 \cdot 8 + \frac{20^{10} (19)}{2} \cdot 3 + \frac{20 \cdot (19) \cdot {(18)}^{3}}{6} \cdot 2 \\ = 160 + 570 + 2280 \\ S_{20} & = 3010 \end{aligned}

\begin{aligned} i)... S_{n} & = n \cdot a + \frac{n (n - 1)}{1 \cdot 2} \cdot a_{1} + \frac{n (n - 1) (n - 2)}{1 \cdot 2 \cdot 3} \cdot a_{2} \\ S_{20} & = 20 \cdot 8 + \frac{20^{10} (19)}{2} \cdot 3 + \frac{20 \cdot (19) \cdot {(18)}^{3}}{6} \cdot 2 \\ = 160 + 570 + 2280 \\ S_{20} & = 3010 \end{aligned}

\begin{aligned} i)... S_{n} & = n \cdot a + \frac{n (n - 1)}{1 \cdot 2} \cdot a_{1} + \frac{n (n - 1) (n - 2)}{1 \cdot 2 \cdot 3} \cdot a_{2} \\ S_{20} & = 20 \cdot 8 + \frac{20^{10} (19)}{2} \cdot 3 + \frac{20 \cdot (19) \cdot {(18)}^{3}}{6} \cdot 2 \\ = 160 + 570 + 2280 \\ S_{20} & = 3010 \end{aligned}

\begin{aligned} i)... S_{n} & = n \cdot a + \frac{n (n - 1)}{1 \cdot 2} \cdot a_{1} + \frac{n (n - 1) (n - 2)}{1 \cdot 2 \cdot 3} \cdot a_{2} \\ S_{20} & = 20 \cdot 8 + \frac{20^{10} (19)}{2} \cdot 3 + \frac{20 \cdot (19) \cdot {(18)}^{3}}{6} \cdot 2 \\ = 160 + 570 + 2280 \\ S_{20} & = 3010 \end{aligned}

4.4 Deret Geometri Tak Hingga

Deret geometri tak hingga didefinisikan sebagai penjumlahan suku-suku pada barisan geometri tak hingga, yaitu di mana kita menghitung semua suku-suku dalam barisan yang tanpa henti ( $U_{1}, U_{2}, \dots$

), dengan simbol rumusnya:

S_{\infty}

Perhatikan dua jenis deret geometri di bawah ini:

\begin{aligned} (1)... 8 + 16 + 32 + \dots = \infty (Tak Terhingga atau Tidak Terdefinisi), dengan r > 1 \\ (2)... 9 + 3 + \frac{1}{3} + \dots = S_{\infty} (Terdefinisi atau bisa dihitung), dengan r < 1 \end{aligned}

Kedua barisan geometri tersebut adalah tak hingga, namun kita hanya bisa menghitung jumlah suku pada barisan geometri turun: ketika $r < 1$

. Berikut rumus-rumus yang bisa digunakan:

$\begin{aligned} (1)... & S_{\infty} = \frac{a}{1 - r}, untuk r < 1 \\ (2)... & r = \frac{U_{n}}{U_{n - 1}} \end{aligned}$

Keterangan:

$S_{n}$

= jumlah suku ke-

n

= suku awal atau

U_{1}

= suku ke-

n

Perhatikan bilangan di bawah ini:

$5, 2 \frac{1}{2}, 1 \frac{1}{4}, \dots$

Tentukanlah jumlah suku-suku dari deret geometri di atas!

PENYELESAIAN.

Diketahui: $a = U_{1} = 5$

Ditanya: $S_{\infty} = \dots ?$

Dijawab:
$\begin{aligned} i)... r & = \frac{U_{n}}{U_{n - 1}} \\ = \frac{U_{2}}{U_{1}} \\ = \frac{2 \frac{1}{2}}{5} \\ = \frac{\frac{5}{2}}{5} \\ = \frac{5}{2} \cdot \frac{1}{5} \\ r & = \frac{1}{2}, kita ketahui r < 1 \end{aligned}$

\begin{aligned} i)... r & = \frac{U_{n}}{U_{n - 1}} \\ = \frac{U_{2}}{U_{1}} \\ = \frac{2 \frac{1}{2}}{5} \\ = \frac{\frac{5}{2}}{5} \\ = \frac{5}{2} \cdot \frac{1}{5} \\ r & = \frac{1}{2}, kita ketahui r < 1 \end{aligned}

\begin{aligned} i)... r & = \frac{U_{n}}{U_{n - 1}} \\ = \frac{U_{2}}{U_{1}} \\ = \frac{2 \frac{1}{2}}{5} \\ = \frac{\frac{5}{2}}{5} \\ = \frac{5}{2} \cdot \frac{1}{5} \\ r & = \frac{1}{2}, kita ketahui r < 1 \end{aligned}

$\begin{aligned} ii)... S_{\infty} & = \frac{a}{1 - r} \\ = \frac{5}{1 - \frac{1}{2}} \\ = \frac{5}{\frac{1}{2}} \\ = 5 \cdot 2 \\ S_{\infty} & = 10 \end{aligned}$

Jadi, $5 + 2 \frac{1}{2} + 1 \frac{1}{4} + \dots = 10$

atau deret

a

b

= beda atau selisih antarsuku

p, q

atau deret

a

r

= rasio atau perbandingan antarsuku

U_{n}

)

S_{n}

atau deret

a

= suku awal barisan

a_{1}

= selisih awal di tingkat 1

a_{2}

= selisih awal di tingkat 2

a_{3}

= selisih awal di tingkat 3

a_{r}

atau deret

a

r

= rasio atau perbandingan antarsuku

U_{n}