Pengertian Baris Bilangan

Barisan Bilangan

Barisan adalah salah satu penyajian pola bilangan dengan bentuk urutan suku berbaris, yang disimbolkan dengan: $U_{n}$

. Berikut bentuk umum barisan.

U_{1}, U_{2}, U_{3}, U_{4}, U_{5}, U_{6}, \dots, U_{n}

3.1 Barisan Aritmetika

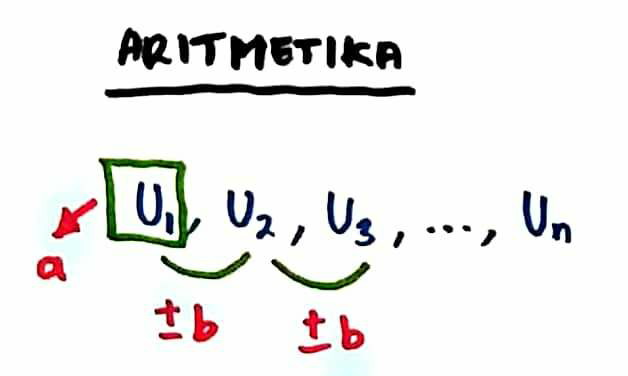
Seperti yang telah disinggung pada jenis pola bilangan, dalam pola aritmetika terdapat ciri: selisih tambah atau kurang yang tetap antarsuku (disebut juga: beda; simbol " $b$

"). Beberapa rumus yang digunakan:

\begin{aligned} (1)... & U_{n} = a + (n - 1) b \\ (2)... & U_{t} = \frac{1}{2} (a + c) \\ (3)... & b = U_{n} - U_{n - 1} \\ (4)... & b = \frac{U_{p} - U_{q}}{p - q} \end{aligned}

$U_{n}$

n

$U_{t}$
= suku tengah dalam barisan
$a$

U_{1}

$b$
= beda atau selisih antarsuku
$c$
= suku terakhir dalam barisan
$p, q$

= sembarang suku bilangan

Perhatikan bilangan di bawah ini:

$3, 7, 11, 15, 19, \dots$

Tentukanlah suku ke-11 dari urutan bilangan di atas!

PENYELESAIAN.

Diketahui:

a = U_{1} = 3

$U_{11} = \dots ?$

$\begin{aligned} i)... b & = U_{n} - U_{n - 1} \\ = U_{2} - U_{1} \\ = 7 - 3 \\ b & = 4 \end{aligned}$

$\begin{aligned} ii)... U_{n} & = a + (n - 1) b \\ U_{11} & = 3 + (11 - 1) 4 \\ U_{11} & = 43 \end{aligned}$

Perhatikan bilangan di bawah ini:

$19, x, 15, y, 11, \dots$

Tentukanlah nilai $x dan y$

dari urutan bilangan di atas!

PENYELESAIAN.

Diketahui: $a = U_{1} = 19$

$x = \dots ?$

$y = \dots ?$

Dijawab:

$\begin{aligned} i)... b & = \frac{U_{p} - U_{q}}{p - q} \\ = \frac{U_{3} - U_{1}}{3 - 1} \\ = \frac{15 - 19}{3 - 1} \\ = \frac{- 4}{2} \\ b & = - 2 \end{aligned}$

$\begin{aligned} ii)... x & = U_{2} \\ x & = 19 + (2 - 1) (- 2) \\ x & = 17 \end{aligned}$

$\begin{aligned} iii)... y & = U_{4} \\ y & = 19 + (4 - 1) (- 2) \\ y & = 13 \end{aligned}$

Jadi, nilai $x dan y$

adalah 17 dan 13.

Dalam barisan aritmetika kita bisa temukan fakta: barisan aritmetika akan naik apabila $b > 0$

b < 0

3.2 Barisan Geometri

Dalam pola geometri, terdapat ciri: adanya rasio yang mengalikan antarsuku. Di bawah ini rumus-rumus yang berlaku dalam barisan geometri:

\begin{aligned} (1)... & U_{n} = a \cdot r^{n - 1} \\ (2)... & r = \frac{U_{n}}{U_{n - 1}} \end{aligned}

Keterangan:

$U_{n}$

n

U_{1}

= rasio atau perbandingan antarsuku terdekat

Perhatikan bilangan di bawah ini:

$4, 16, 64, 256, \dots$

Tentukanlah rumus nilai $U_{n}$

dari barisan bilangan di atas!

PENYELESAIAN.

Diketahui: $a = U_{1} = 4$

$U_{n} = \dots ?$

Dijawab:
$\begin{aligned} i)... r & = \frac{U_{n}}{U_{n - 1}} \\ = \frac{U_{2}}{U_{1}} \\ = \frac{16}{4} \\ r & = 4 \end{aligned}$

$\begin{aligned} ii)... U_{n} & = a \cdot r^{n - 1} \\ = 4 \cdot 4^{n - 1} \\ = 4 \cdot \frac{4^{n}}{4} \\ U_{n} & = 4^{n} \end{aligned}$

\begin{aligned} ii)... U_{n} & = a \cdot r^{n - 1} \\ = 4 \cdot 4^{n - 1} \\ = 4 \cdot \frac{4^{n}}{4} \\ U_{n} & = 4^{n} \end{aligned}

\begin{aligned} ii)... U_{n} & = a \cdot r^{n - 1} \\ = 4 \cdot 4^{n - 1} \\ = 4 \cdot \frac{4^{n}}{4} \\ U_{n} & = 4^{n} \end{aligned}

U_{4} = 135

5

\dots

PENYELESAIAN.

Diketahui: $a = U_{1} = 5$

U_{4} = 135

$r = \dots ?$

Dijawab:
$\begin{aligned} i)... \frac{U_{4}}{U_{1}} & = \frac{a \cdot r^{3}}{a} \\ \frac{135}{5} & = r^{3} \\ \sqrt[3]{27} & = r \\ r & = 3 \end{aligned}$

\begin{aligned} i)... \frac{U_{4}}{U_{1}} & = \frac{a \cdot r^{3}}{a} \\ \frac{135}{5} & = r^{3} \\ \sqrt[3]{27} & = r \\ r & = 3 \end{aligned}

\begin{aligned} i)... \frac{U_{4}}{U_{1}} & = \frac{a \cdot r^{3}}{a} \\ \frac{135}{5} & = r^{3} \\ \sqrt[3]{27} & = r \\ r & = 3 \end{aligned}

3.3 Barisan Aritmetika Bertingkat

Barisan aritmetika bertingkat membahas lebih jauh dalam tingkatan lebih lanjut, bagaiman kita mencari urutan bilangan atau penyelesaian lain bila menemukan suatu barisan aritmetika dengan selisih tetap di tingkat lebih dari satu (tingkat dua, tingkat tiga, dan seterusnya).

Kita telah mengetahui jika $U_{n} = a + (n - 1) b$

(rumus barisan aritmetika) hanya berlaku di tingkat satu: ketika selisih tetap ditemukan di tingkat satu. Lalu bagaimana jika selisih belum tetap di tingkat satu atau kemungkinan penyelesaian di tingkat lebih dari satu?

Untuk menjawab pertanyaan di atas, di sinilah barisan aritmetika bertingkat akan dibahas. Sebelum menginjak pada rumus penyelesaiannya, mari kita perhatikan cara mengenali di tingkat berapa barisan aritmetika bertingkat.

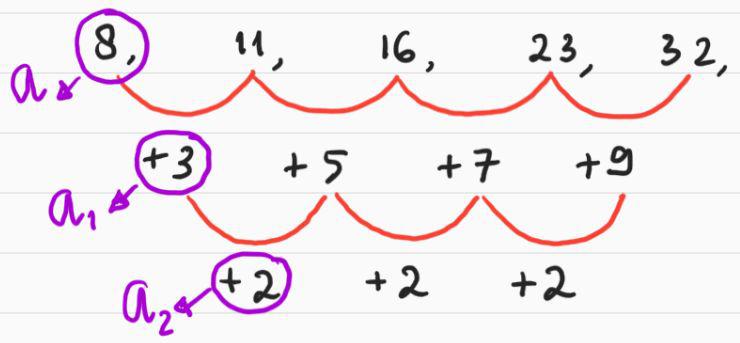
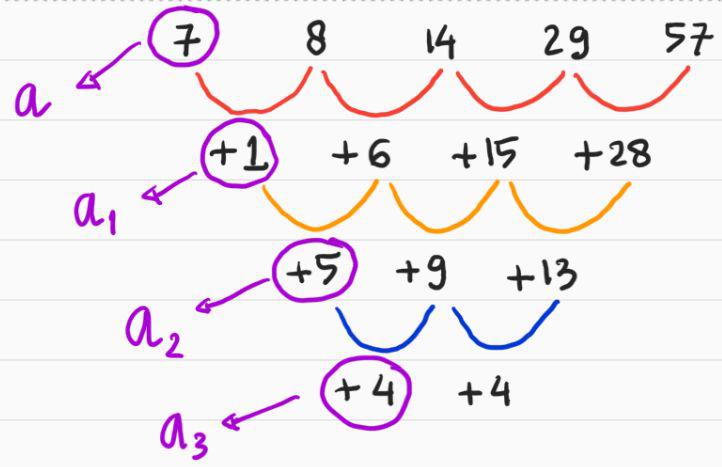
Cara Mengetahui Tingkat Barisan Aritmetika

Carilah selisih antarsuku secara manual, dan lihat apakah selisih telah tetap atau masih berubah di tingkat pertama percobaan.
Jika selisih telah tetap di percobaan pertama (tingkat satu), maka bisa gunakan rumus barisan aritmetika biasa.
Jika selisih masih berubah di tingkat satu, lanjut di bawahnya, carilah selisih antarsuku di tingkat setelahnya. Kuncinya adalah selisih tetap di tingkat berapa, dan itulah indikator tingkatan barisan aritmetika bertingkat.

Setelah kita mengenali langkah awal mengenali persoalan dengan cara di atas, kita bisa gunakan beberapa rumus yang berlaku dalam barisan aritmetika bertingkat (yang dimulai dari tingkat dua, tiga, dan seterusnya).

$\begin{aligned} (1)... & U_{n} = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} \\ (2)... & U_{n} = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} + \frac{(n - 1) (n - 2) (n - 3)}{1 \cdot 2 \cdot 3} \cdot a_{3} \\ (3)... & U_{n} = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} + \dots + \frac{(n - 1) (n - 2) \dots}{1 \cdot 2 \cdot \dots} \cdot a_{r} \end{aligned}$

Keterangan:

(1) = rumus $U_{n}$

tingkat 2
(2) = rumus $U_{n}$
tingkat 3
(3) = rumus $U_{n}$

r

1, 2, \dots, r

)
$a$
= suku awal barisan utama
$a_{1}$
= selisih awal di tingkat 1
$a_{2}$
= selisih awal di tingkat 2
$a_{3}$
= selisih awal di tingkat 3
$a_{r}$

r

Perhatikan bilangan di bawah ini:

$8, 11, 16, 23, 32, \dots$

Tentukanlah nilai $U_{20}$

dari barisan bilangan di atas!

PENYELESAIAN.

Diketahui: barisan aritmetika tingkat 2 ; $a = 8$

a_{1} = 3

a_{2} = 2

$U_{20} = \dots ?$

Dijawab:

\begin{aligned} i)... U_{n} & = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} \\ U_{20} & = 8 + (20 - 1) \cdot 3 + \frac{(20 - 1) (20 - 2)}{1 \cdot 2} \cdot 2 \\ = 8 + (19) \cdot 3 + \frac{(19) (18)}{2} \cdot 2 \\ = 8 + 57 + 342 \\ U_{20} & = 407 \end{aligned}

\begin{aligned} i)... U_{n} & = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} \\ U_{20} & = 8 + (20 - 1) \cdot 3 + \frac{(20 - 1) (20 - 2)}{1 \cdot 2} \cdot 2 \\ = 8 + (19) \cdot 3 + \frac{(19) (18)}{2} \cdot 2 \\ = 8 + 57 + 342 \\ U_{20} & = 407 \end{aligned}

Perhatikan bilangan di bawah ini:

$7, 8, 14, 29, 57, \dots$

Tentukanlah nilai $U_{6}$

dari barisan bilangan di atas!

PENYELESAIAN.

Diketahui: barisan aritmetika tingkat 3 ; $a = 7$

a_{1} = 1

a_{2} = 5

a_{3} = 4

$U_{6} = \dots ?$

Dijawab:
$\begin{aligned} i)... U_{n} & = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} + \frac{(n - 1) (n - 2) (n - 3)}{1 \cdot 2 \cdot 3} \cdot a_{3} \\ U_{6} & = 7 + (6 - 1) \cdot 1 + \frac{(6 - 1) (6 - 2)}{1 \cdot 2} \cdot 5 + \frac{(6 - 1) (6 - 2) (6 - 3)}{1 \cdot 2 \cdot 3} \cdot 4 \\ = 7 + 5 (1) + \frac{(5) {(4)}^{2}}{2} \cdot 5 + \frac{(5) (4) (3)}{6^{2}} \cdot 4^{2} \\ = 7 + 5 + 50 + 40 \\ U_{6} & = 102 \end{aligned}$

\begin{aligned} i)... U_{n} & = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} + \frac{(n - 1) (n - 2) (n - 3)}{1 \cdot 2 \cdot 3} \cdot a_{3} \\ U_{6} & = 7 + (6 - 1) \cdot 1 + \frac{(6 - 1) (6 - 2)}{1 \cdot 2} \cdot 5 + \frac{(6 - 1) (6 - 2) (6 - 3)}{1 \cdot 2 \cdot 3} \cdot 4 \\ = 7 + 5 (1) + \frac{(5) {(4)}^{2}}{2} \cdot 5 + \frac{(5) (4) (3)}{6^{2}} \cdot 4^{2} \\ = 7 + 5 + 50 + 40 \\ U_{6} & = 102 \end{aligned}

\begin{aligned} i)... U_{n} & = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} + \frac{(n - 1) (n - 2) (n - 3)}{1 \cdot 2 \cdot 3} \cdot a_{3} \\ U_{6} & = 7 + (6 - 1) \cdot 1 + \frac{(6 - 1) (6 - 2)}{1 \cdot 2} \cdot 5 + \frac{(6 - 1) (6 - 2) (6 - 3)}{1 \cdot 2 \cdot 3} \cdot 4 \\ = 7 + 5 (1) + \frac{(5) {(4)}^{2}}{2} \cdot 5 + \frac{(5) (4) (3)}{6^{2}} \cdot 4^{2} \\ = 7 + 5 + 50 + 40 \\ U_{6} & = 102 \end{aligned}

\begin{aligned} i)... U_{n} & = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} + \frac{(n - 1) (n - 2) (n - 3)}{1 \cdot 2 \cdot 3} \cdot a_{3} \\ U_{6} & = 7 + (6 - 1) \cdot 1 + \frac{(6 - 1) (6 - 2)}{1 \cdot 2} \cdot 5 + \frac{(6 - 1) (6 - 2) (6 - 3)}{1 \cdot 2 \cdot 3} \cdot 4 \\ = 7 + 5 (1) + \frac{(5) {(4)}^{2}}{2} \cdot 5 + \frac{(5) (4) (3)}{6^{2}} \cdot 4^{2} \\ = 7 + 5 + 50 + 40 \\ U_{6} & = 102 \end{aligned}

\begin{aligned} i)... U_{n} & = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} + \frac{(n - 1) (n - 2) (n - 3)}{1 \cdot 2 \cdot 3} \cdot a_{3} \\ U_{6} & = 7 + (6 - 1) \cdot 1 + \frac{(6 - 1) (6 - 2)}{1 \cdot 2} \cdot 5 + \frac{(6 - 1) (6 - 2) (6 - 3)}{1 \cdot 2 \cdot 3} \cdot 4 \\ = 7 + 5 (1) + \frac{(5) {(4)}^{2}}{2} \cdot 5 + \frac{(5) (4) (3)}{6^{2}} \cdot 4^{2} \\ = 7 + 5 + 50 + 40 \\ U_{6} & = 102 \end{aligned}

\begin{aligned} i)... U_{n} & = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} + \frac{(n - 1) (n - 2) (n - 3)}{1 \cdot 2 \cdot 3} \cdot a_{3} \\ U_{6} & = 7 + (6 - 1) \cdot 1 + \frac{(6 - 1) (6 - 2)}{1 \cdot 2} \cdot 5 + \frac{(6 - 1) (6 - 2) (6 - 3)}{1 \cdot 2 \cdot 3} \cdot 4 \\ = 7 + 5 (1) + \frac{(5) {(4)}^{2}}{2} \cdot 5 + \frac{(5) (4) (3)}{6^{2}} \cdot 4^{2} \\ = 7 + 5 + 50 + 40 \\ U_{6} & = 102 \end{aligned}

\begin{aligned} i)... U_{n} & = a + (n - 1) \cdot a_{1} + \frac{(n - 1) (n - 2)}{1 \cdot 2} \cdot a_{2} + \frac{(n - 1) (n - 2) (n - 3)}{1 \cdot 2 \cdot 3} \cdot a_{3} \\ U_{6} & = 7 + (6 - 1) \cdot 1 + \frac{(6 - 1) (6 - 2)}{1 \cdot 2} \cdot 5 + \frac{(6 - 1) (6 - 2) (6 - 3)}{1 \cdot 2 \cdot 3} \cdot 4 \\ = 7 + 5 (1) + \frac{(5) {(4)}^{2}}{2} \cdot 5 + \frac{(5) (4) (3)}{6^{2}} \cdot 4^{2} \\ = 7 + 5 + 50 + 40 \\ U_{6} & = 102 \end{aligned}

kita punya definisi jelas tentang deret?

Deret adalah penjumlah suku dalam suatu barisan, yang disimbolkan dengan: $S_{n}$

. Kita bisa melihat bentuk umumnya di bawah ini:

U_{1} + U_{2} + U_{3} + \dots + U_{n} = S_{n}

4.1 Deret Aritmetika

Deret aritmetika merupakan penjumlahan suku-suku dalam suatu barisan aritmetika. Masih ingat ciri barisan aritmetika, 'kan?

$\begin{aligned} (1)... & S_{n} = \frac{n}{2} (a + U_{n}) \\ (2)... & S_{n} = \frac{n}{2} (2 a + (n - 1) b) \\ (3)... & b = U_{n} - U_{n - 1} \\ (4)... & b = \frac{U_{p} - U_{q}}{p - q} \end{aligned}$

Keterangan:

$S_{n}$

n

atau deret
$a$

U_{1}